AIG

Navigate firm data through the following pages:

Analyst Listing Primary Input Data
Derived Input Data Valuation Model Outcomes

Analyst Listing

The following analysts provide coverage for the subject firm as of May 2016:

Broker Analyst Analyst Email
Wells Fargo Securities Elyse Greenspan elyse.greenspan@wellsfargo.com
FBR Capital Markets & Co Randy Binner rbinner@fbr.com
RBC Capital Markets Mark Dwelle mark.dwelle@rbccm.com
Bernstein Research Josh Stirling josh.stirling@bernstein.com
Atlantic Equities John Heagerty j.heagerty@atlantic-equities.com
Piper Jaffray John Nadel john.m.nadel@pjc.com
Sandler O’Neill & Partners Paul Newsome pnewsome@sandleroneill.com
Janney Montgomery Scott Larry Greenberg lgreenber@janney.com
Keefe Bruyette & Woods Meyer Shields mshields@kbw.com
William Blair Adam Klauber aklauber@williamblair.com
BMO Capital Markets Charles J. Sebaski charles.sebaski@bmo.com
Deutsche Bank Research Joshua Shanker joshua.shanker@db.com
Credit Suisse Ryan Tunis ryan.tunis@credit-suisse.com

Return to top of page

Primary Input Data

 

Return to top of page

Derived Input Data

Derived Input

Label

2015  Value

2016  Value

Equational Form
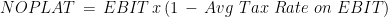Net Operating Profit Less Adjusted Taxes NOPLAT   3,981  1,883 NOPLAT\, =\, EBIT\, x\, (1 \,-\, Avg \,\,Tax\,\, Rate\,\, on\,\, EBIT)
Free Cash Flow FCF  2,877  2,383 FCF\,=NOPLAT\,+\,Non-Cash\,Expenses-\Delta NWC\,-\,NCS
Tax Shield TS  417  (406) TS\,=\,Interest\,\,Paid\,\,x\,\, Avg \,\,Tax\,\,Rate\,\, on\,\, Pre-Tax\,\, Income
Invested Capital IC  352,886  355,360 IC\,=\,Fixed\,\,Operating\,\,Assets\,\,+\,\,Net\,\, Working\,\, Capital
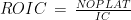Return on Invested Capital ROIC 1.13% 0.53% ROIC\,=\,\frac { NOPLAT }{ IC }
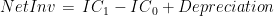Net Investment NetInv  107,920  2,474 NetInv\,=\,{ {IC}_{1}}-{{IC}_{0}}+Depreciation
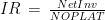Investment Rate IR 2711.15% 131.38% IR\,=\,\frac {NetInv}{NOPLAT}
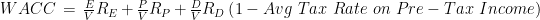
Weighted Average Cost of Capital WACCMarket -3.46% -2.44% WACC\,=\,\frac { E }{ V } { R }_{ E }\,+\,\frac { P }{ V } { R }_{ P }\,+\,\frac { D }{ V } { R }_{ D }\left( 1- Avg\,\, Tax\,\,Rate\,\,on\,\,Pre-Tax\,\,Income \right)
 WACCBook  7.90% 7.80%
Enterprise value EVMarket  104,699  94,921  EV\,=\,Market\,\,Cap\,\,Equity\,+\,\,Long\,\,Term\,\,Debt\,-\,Cash
 EVBook  99,919  91,695
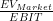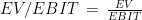EV/EBIT Multiple \frac{EV_{Market}}{EBIT}  17.10  32.77 EV/EBIT\,=\,\frac { EV}{ EBIT}
Long-Run Growth g = IR x ROIC
   30.58%   0.70% Long-run growth rates of the income variable  are used in the Continuing Value portion of the valuation models.
 g = % 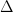\Delta GDP    2.50%   2.50%

Return to top of page

Valuation Model Outcomes

The outcomes presented in this study are the result of original input data, derived data, and synthesized inputs and, depending on the equational form of any particular valuation model, may result in irrelevant or implausible results.  For example, in the event WACC < g, the value of this term, often found in the denominator of an equation’s continuation value term, will be expressly negative and may result in a negative overall valuation for the firm.  In the event of a WACC < g relation, the model form as applied to the subject firm offers an irrelevant outcome.

Valuation Model Type

Label

Equational form
Key Value Driver (NOPLAT) KVD (NOPLAT) { Value }_{ DCF/KVD }=\sum { \frac { NOPLAT_{ t } }{ { \left( 1+WACC \right) }^{ t } } +\frac { \frac { { NOPLAT }_{ 1 }\left( 1-\frac { g }{ ROIC } \right) }{ WACC-g } }{ { \left( 1+WACC \right) }^{ t } } }
 
Key Value Driver (FCF) KVD (FCF)
{ Value }_{ DCF/KVD }=\sum { \frac { FCF_{ t } }{ { \left( 1+WACC \right) }^{ t } } +\frac { \frac { { NOPLAT }_{ 1 }\left( 1-\frac { g }{ ROIC } \right) }{ WACC-g } }{ { \left( 1+WACC \right) }^{ t } } }
 
Free Cash Flow FCF { Value }_{ DCF/FCF }=\sum { \frac { FCF_{ t } }{ { \left( 1+WACC \right) }^{ t } } +\frac { \frac { { FCF }_{ 1 }}{ WACC-g } }{ { \left( 1+WACC \right) }^{ t } } }
 
Economic Profit ECON π { Value }_{ { ECON\pi } }= I{ C }_{ 0 }+\sum { \frac { { IC }_{ t-1 }(ROI{ C }_{t}-WAC{C}_{t}) }{ { \left( 1+WACC \right) }^{ t } }+ \frac {\frac { I{C}_{0}\ x\ (ROI{C}_{1}\ -\ WAC{C}_{1}) }{ WACC-g } }{ { \left( 1+WACC \right) }^{ t } } }
 
Adjusted Present Value APV { Value }_{ APV }=\sum { \frac { FCF_{ t } }{ { \left( 1+{ k }_{ u } \right) }^{ t } } +\frac { \frac { { FCF }_{ 1 }}{ { k }_{ u }-g } }{ { \left( 1+{ k }_{ u } \right) }^{ t } } } +\sum { \frac { { TS }_{ t } }{ { \left( 1+{ k }_{ tax } \right) }^{ t } } +\frac { \frac { { TS }_{ 1 }}{ { k }_{ tax }-g } }{ { \left( 1+{ k }_{ tax } \right) }^{ t } } }
 
Forward Market Multiple FMM { Value }_{ DCF/FMM}=\sum { \frac { FCF_{ t } }{ { \left( 1+WACC \right) }^{ t } } +\frac { { EBIT }_{ 1 }\,{x}\,{FMM}}{ { \left( 1+WACC \right) }^{ t } } }{\,\,\,; \,\,FMM\,=\,\frac{{EV}_{t=0}}{{EBIT}_{t=0}}}
 

Return to top of page